Quartz Crystal Filter Design

Equivalent Circuit Determination of Quartz Crystals

Before we may design a crystal filter it is necessary to know the crystal's data. Unfortunately this information is not in the datasheet - or we have no datasheet because the crystals were bought on a market some decades ago ...

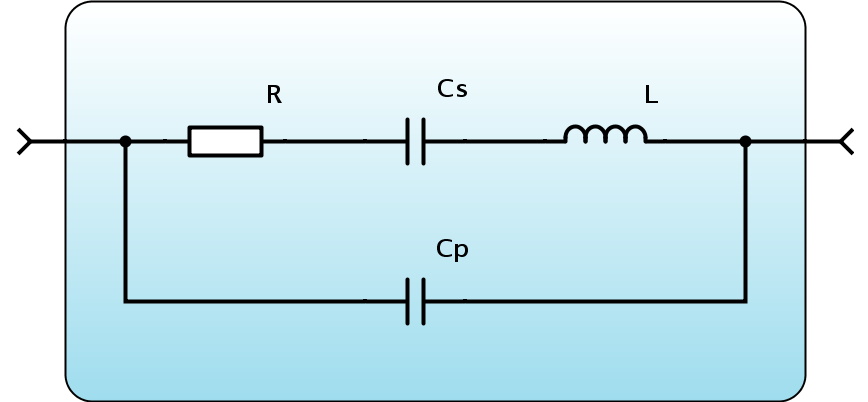
A quartz crystal and its equivalent circuit

As you may have guessed from the equivalent circuit above, a quartz crystal has a series resonance (Cs and L) as well as a parallel resonance. This may be observed very well, when doing a frequency sweep, using the quartz as a series element. In order to determine these four values (R, Cs, L, Cp) one measurement is not enough. We use a small testfix for the frequency sweep. Building such a thing allows for stable electronic and mechanical conditions, leading to reliable and reproduceable results.

Those four values may be obtained by four measurements :

• Holder Capacitance : Cp
• Series resonance frequency : fs
• Parallel resonance frequency : fp
• The dynamic Losses : R

Measurement Adapter in Action, Details about this test fixture

Measure Cp

The easiest way to get this value is the use of a RLC-Meter. This has the ad- vantage, that no calibration is neces- sary. (Except zero).

Measure fs and fp

The Series / Paralle resonance frequency may be measured by a lot of setups. A vector network analyser is of course the luxury version, but you may as well use a generator and a scope, a spectrum analyser with a generator or any linear combination thereof. The quartz crystal is connected in series between the source and the load. We are intersted in the maximum amplitude (fs, where XL = XCs) and the minimum (fp, where XL and XCs, XCp form a block).

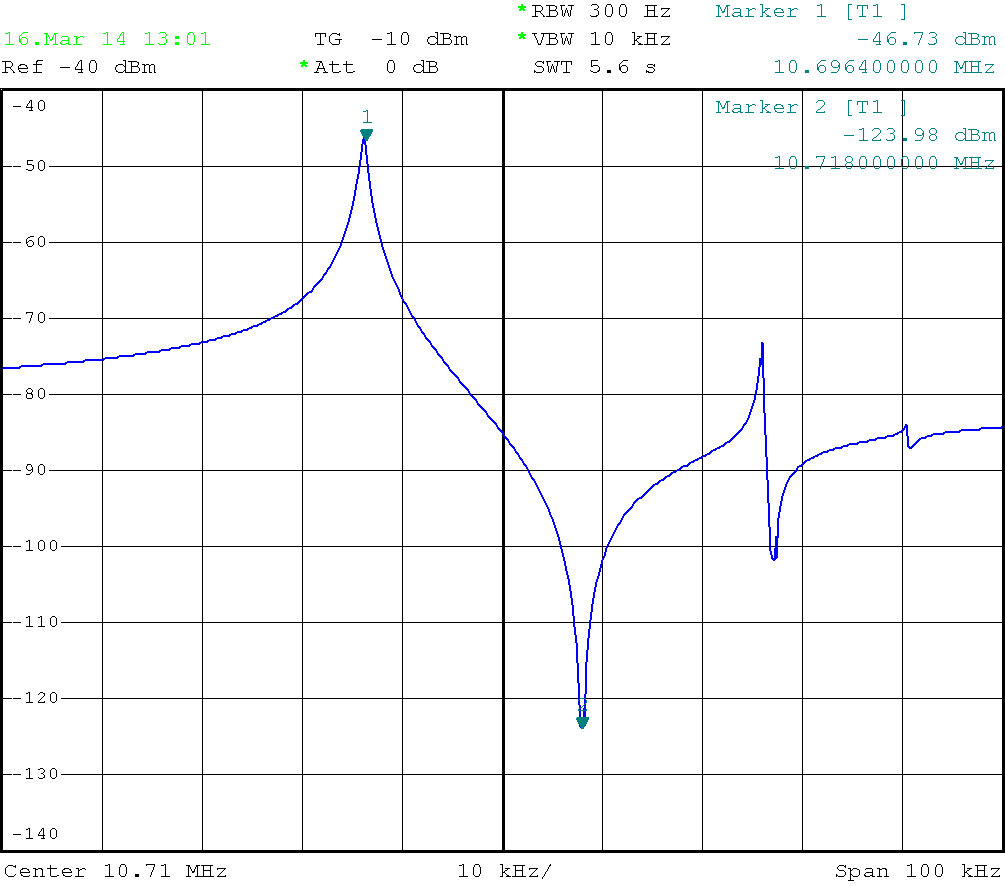
Measured Amplitude Response of a Quartz Crystal in the test fixture

Measure Insertion Loss at fs

This measurement targets the internal "Resistor". We measure exactly at the series resonance frequency, because there, XL and XCs sum up to zero. So what is left, is a (resistive) voltage divider, consisting of your source, the R from the quartz and the load. Whereas source and load are mostly 50 Ω. Please keep in mind to calibrate or to measure the difference (shorted / quartz inserted).

PROCEED HERE TO LADDER FILTER CALCULATOR

The Mathematics behind

Credits :

The Visualisation uses https://www.mathjax.org/

✈ Share your thoughts