• Home
• ช้างเผือก
• Electronics
• Bijoux
• Pictures
• Foodlab
• Links
• Sitemap
• Terms
•  Print
•  Email
• 
• 

---

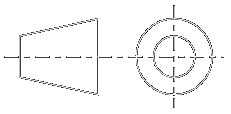
DIELECTRIC COAXIAL RESONATOR

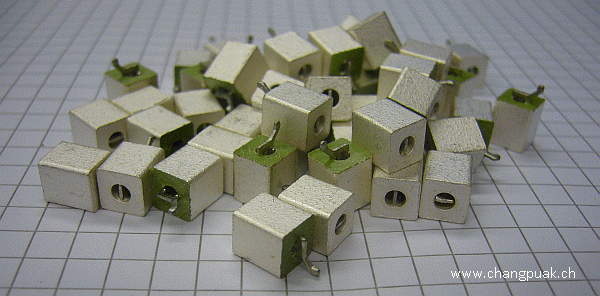
Fig 1: Dielectric Coaxial Resonators

Coaxial line elements can be used below resonance to simulate high-Q , temperature stable, compact inductors. More precisely, shorted coax lines will exhibit an inductive reactance when used below quarter-wave resonance and will aproximate the behaviour of an ideal inductance or coil over a limited frequency range. As the operating frequency approaches the SRF (Self Resonance Frequency) the approximtion will be less valid. An exact equivalent circuit is complex and would include parasitic elements resulting
from a transition from the printed circuit board.

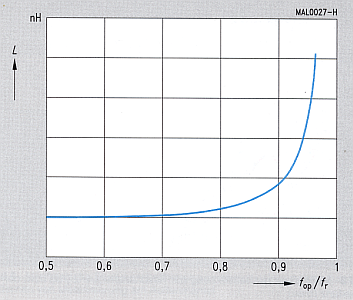
Fig 2: Inductance of coaxial resonators versus operating frequency.
[Siemens Matsushita Components]

MEASURE DATA OF DIELECTRIC RESONATOR

Similiar to the approach on Designing Crystal Filters we need an adapter which
can be easily made of a piece of FR-4 and a milling cutter.

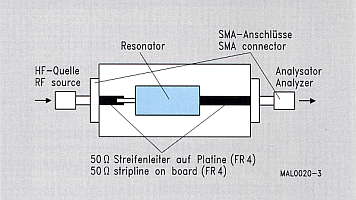
Fig 3: Schematics of Measurement Adapter
[Siemens Matsushita Components]

Fig 4: Realised Circuit of Measurement Adapter

Set the Networkanalyser (or Spectrum Analyser with Tracking generator or
whatever you use) to maximum Span. Somewhere a drop will be observed.
Zoom in to measure the Frequency and the 3dB Bandwidth. Our 'unknown Device'
produced something like that on the Picture below:

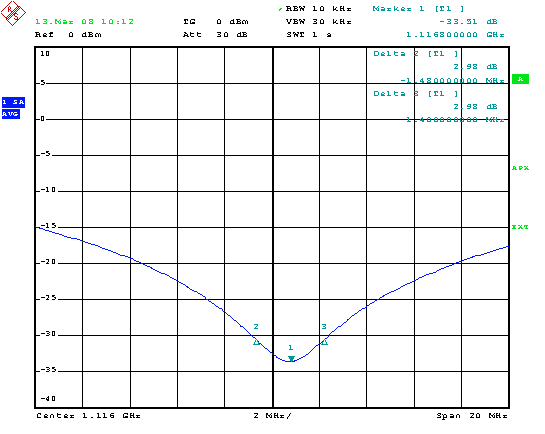
Fig 5: Frequency Response, measured with R&S FSP

From the measurement above we know : f_center = 1116.8 MHz,
BW(3dB) = 2.88 MHz
Therefore we calculate the Q as :

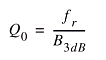
... in our case Q = 388

In order to know more about this DCR we need to take measurements.
The Picture below shows what to measure.

... and the table below shows what we measured at our device ...

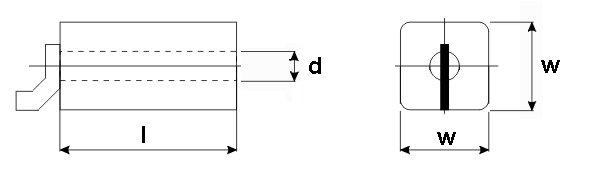
Fig 6: Geometry of Dielectric Coaxial Resonator

DIMENSION	LENGTH [mm]
LENGTH [l]	7.20
WIDTH [w]	6.10
INNER DIAMETER [d]	2.60

RELATIVE PERMITTIVITY OF MATERIAL : Ε_r

With the knowledge of the Dimensions we may calculate the relative
permittivity of the ceramic Material.

x = 4 for λ/4 (shorted at the end) or x = 2 for λ/2 (end plane not conducting)
c = speed of light, 3 * 10⁸ m/s
f₀ = Centerfreq. (measured above)
l = Length

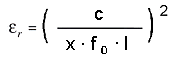
... in our case Ε_r = 86.997

CHARACTERISTIC IMPEDANCE : Z₀

µ_r : relative magnetic permeability of the material, here : µ_r = 1
w : width of resonator
d : internal diameter of resonator
g : geometric factor, here : g = 1.07

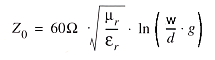
... in our case Z₀ = 5.9748 Ω

CALCULATING THE DATA OF THE EQUIVALENT NETWORK

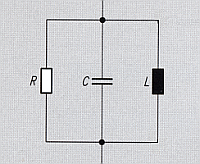
Fig 7: Equivalent Network
[Siemens Matsushita Components]

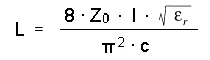
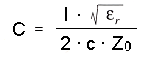
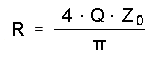
... in our case :

PART	VALUE
Resistor [Ω]	2949.9
Inductor [nH]	1.048
Capacitor [pF]	18.733

CALCULATE DATA OF DIELECTRIC RESONATOR

Length λ/4 (end shorted)

f0 [MHz]
Bandwidth [MHz]
Dimension l [mm]
Dimension w [mm]
Dimension d [mm]
Q
Relative Permittivity Εr
R [Ω]
L [nH]
C [pF]
Z [Ω]

---

Share your thoughts.

This is not suiteable to contact the author. Use the "email" function instead.